Problém čtyř barev
autor:Martina Barešová
„Stačí čtyři barvy na obarvení libovolné politické mapy tak, aby žádné dva sousedící státy nebyly obarveny stejnou barvou?“
Tento zajímavý problém patří do takzvané teorie grafů,která je samostatnou matematickou disciplínou.Pomocí teorie grafů lze dokázat, že pro obarvení libovolné mapy tak, aby dvě sousední země nebyly obarveny stejnou barvou, nám postačí čtyři barvy.
Tento problém poprvé zmínil A.F.Möbius v roce 1840.Matematikové v jeho době dokázali,že pět barev zaručeně stačí k obarvení každé mapy,dlouho se však nevědělo,zda pouhé čtyři barvy stačí na všechny příklady,jaké mohou nastat.
Problém čtyř barev vzdoroval úsilí matematiků až do roku 1976.kdy američtí matematici Apple a Haken dokázali,že čtyři barvy opravdu stačí k obarvení libovolné mapy.Pomocí počítače vymodelovali 1936 možných konfigurací a dokázali,že tyto konfigurace představují všechny možnosti a u každé mapy ukázali,že pro její vybarvení stačí čtyři barvy.
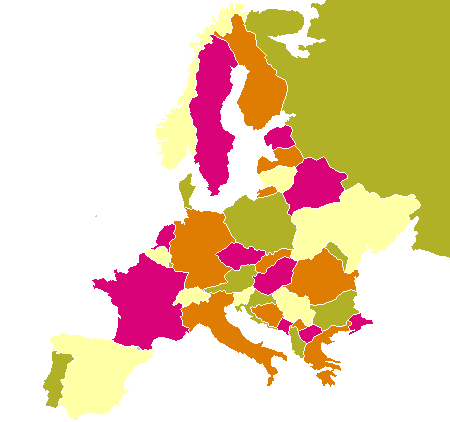
Protože se jedná o problém z tzv.teorie grafů,převádí matematikové mapu na graf.V každém státě se vyznačí bod(třeba hlavní město) a tyto body se pospojují tak,aby byly spojené ty body,jejichž oblasti spolu sousedí.Pak se body vybarví tak,aby žádné dva body spojené čárou neměly stejnou barvu.
Nikdy předtím nebyl klasický matematický problém vyřešen jinak než lidským myšlením,proto se brzy začali ozývat matematikové s otázkami,zda se tento důkaz opravdu počítá.Co když počítačový program obsahoval programátorskou chybu a nebo neprošel všechny možnosti?Nicméně důza je tak obsáhlý,něž aby mohl být zkontrolován ručně.Důkaz počítačového programu má 56 stran textu a 342 obrázků.K tomu,aby se prokázalo,že je nepravdivá,by muel být ukázán příklad určité mapy vyžadující více než 4 barvy.
Zdroj: https://fyzmatik.pise.cz/720-problem-4-barev.h
